The Bedrock of Modern Portfolio Theory - Finance Papers 1.1
Markowitz’s 1952 paper is the basis of many commonly accepted financial and economic ideas: rational investors, probabilistic returns, mean-variance optimization — there’s a lot to unpack here.
Paper Covered:
“Portfolio Selection”, H. Markowitz (1952)
For those of you who’ve read ahead: we will get to Sharpe (1964), Fama (1970), and Black & Scholes (1973) in a few posts.
Their works are built upon the foundations we’ll cover today.
A Novel Idea: Optimizing Portfolios
Harry Markowitz, the father of modern portfolio theory, grounds his 1952 paper on three core ideas:
Investors act rationally based on probabilistic beliefs
Investors seek to maximize returns
Investors are risk averse — they seek to minimize variance
Later papers in this series will build upon or pick apart these ideas that sit at the center of most Modern Portfolio Theory.
Where do these core assumptions come from?
Markowitz credits J.B. Williams, the “Father of Dividend (DCF) Investing”, as the starting point for these ideas.
Williams (1938) argued that “the investor does (or should) maximize the discounted (or capitalized) value of future returns.” His book is the genesis of the rational investor who sits at the center of most modern portfolio and economic theory. But it fell short by not acknowledging that stocks could be correlated — surprising given what happened in 1929-1933 — which is something Markowitz would come back to later remedy.
It was The Great Depression of the 1930s and the rampant speculation in the 1920s which led to it that most shaped the views of Williams and every other investor and economist of the era. Many came to the same conclusion: greater rigor needs to be brought to valuations and the investment decision making process.
The Nobel Dream Team
The wealthy investment advisor Alfred Cowles III was another product of the boom-bust 1920s and 1930s. Following the “stock market crash of 1929, he realized that he did not understand the workings of the economy, and so in 1931 he stopped publishing his market advisory letter and began his research on stock market forecasting”. Cowles sought to use the greatest economic minds of the era to bring a quantitative approach and formal theory to financial market analysis.
The “Cowles Commission” (now the Cowles Foundation) brought together some of the greatest minds of the era, including a slew of Noble Laureates including Jacob Marschak and Tjalling Koopmans of the University of Chicago’s economics department.
Marschak, the “Father of Econometrics”, and Koopmans, a pioneer in linear programming, would have a profound impact on Markowitz as instructors at the University of Chicago then as mentors and peers on the Cowles Commission.
After being advised by Marschak to speak with Koopmans about his degree thesis — which would go on to become his famous 1952 paper — Markowitz joined the Cowles commission as a student member.
A Scattered Plot of Risk and Return
The idea that returns on capital should be linked to risk is not new, and how these concepts relate to individual investments has been well understood for thousands of years. What was less understood was how risks related to one another in a portfolio of assets. to combine different sources of return to create an optimal portfolio of assets.
To solve this issue, Markowtiz made a key assumption which led to his “aha moment”…
Returns on a security are like random variables. That means that the return on the portfolio was a weighted average of the returns of the individual securities…but I didn’t know what the variance or standard deviation of the weighted sum was, so I got a book off the library shelf…and looked up the formula for the variance of weighted sum, and there it was: covariances, correlations.
I had the ‘aha’ moment that the variability of the riskiness of the portfolio depended not only on the volatility of the individual securities, but [also] to the extent which they went up and down together.
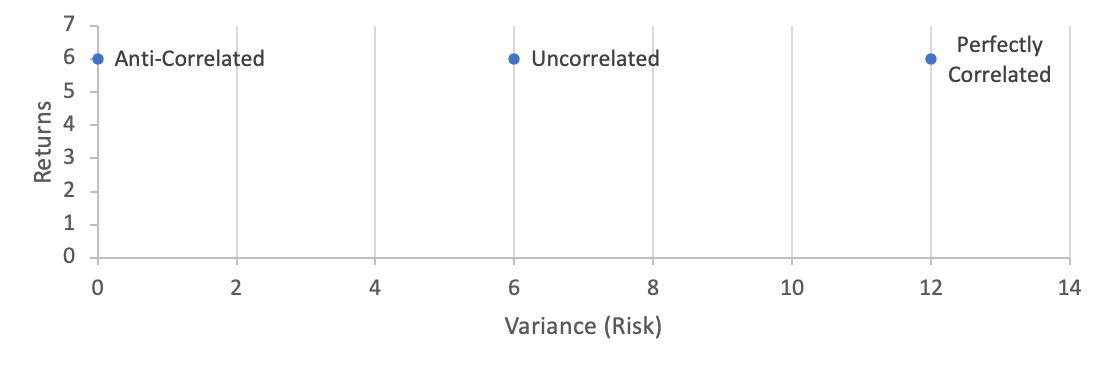
Common knowledge at the time just assumed that total diversification could eliminate any correlation between stocks, but this could lead to investing in a lot of stocks which are highly correlated — something Williams had previously overlooked.
By accounting for the relationship between the investments in a portfolio, one could avoid unknowingly “putting all their eggs in one basket.”
This fact is best represented with math (sorry in advance to my philosophy majors, like Markowitz once was)

The above equations demonstrate two points of intuition that we’ll spend the next 70 years of economic thought debating:
A (rational) investor clearly wants to select the portfolio with the maximum return and the minimum risk.
If the investor select a portfolio with less correlated assets, the riskiness of the overall portfolio decreases.
It’s easier expand the intuition from above by plotting the risks and returns for all the possible portfolio for all securities (aka the “investable universe”). Doing so results in a big blob of portfolios each with different characteristics.
The middle of the blob is unimportant, because as demonstrated above, there must necessarily be less risky portfolios. Additionally, the edges on the bottom half of the blob can be excluded, because there are better returns for the same level of risk by moving to the upper edge.

The upper edge of the investable universe blob is the “Efficient Frontier” meaning that each portfolio along this edge has the maximum return for a given level of risk.
With this graph, Markowitz has given an investor with sufficient computing power the ability to calculate the exact asset allocation to maximize his return (r1, r2, r3) for his given risk tolerance (σ1, σ2, σ3). Markowitz would go on to apply some of Dantzig’s linear optimization methods in later works which expanded on his core idea of maximizing risk-return for a portfolio.
How has this paper impacted the world of Finance?
The long-lasting impact of Portfolio Selection has been the mathematical rigor brought to the investing and economic communities. As we’ll see later, when the core ideas here are combined with the later works of Treynor, Sharpe, and Miller, we can trace the birth of Capital Asset Pricing, options pricing models, John Bogle’s 60/40 portfolio, algorithmic trading, and so much more.
Markowitz acknowledges the work left to be done with respect to bringing probabilities to security analysis and creating factor models to explain market prices. Next week, we’ll pick up right where his work leaves off with the introduction of Jack Treynor and William Sharpe.
To wrap this up, I’ll return to Markowitz’s 1952 conclusion: “I will not pursue [probabilities and factor models] here, for this is another story. It is a story of which I have read only the first page of the first chapter.”
Here’s a preview of what we’re look at next time:
The Next Chapter: Capital Asset Prices
Adding another page to the story
In 1959, Markowitz expanded on his 1952 paper by writing the book Portfolio Selection: Efficient Diversification of Investments. It combines book combined his 1952 work with that of his mentors from the Cowles Commission and peers at the RAND corporation (namely Dantzig’s innovations in linear programming).
Portfolio Selection (1959) would go on to influence and instruct thousands of students, including a masters student at UCLA, William F. Sharpe, who credited the work with teaching him the matrix algebra (a key to liner optimization) used in his later Nobel Prize winning works.
Some Sources:
“The Cowles Commission's Contributions to Econometrics at Chicago, 1939-1955”, C.F. Christ (1994)
“The Economics Book”, Steven Medema (2019)
Nobel Memorial Lecture, Tjalling C. Koopmans (1975)
Nobel Memorial Lecture, Harry Markowitz (1990)
Nobel Memorial Lecture, William F. Sharpe (1990)
Extra Bits:
The valuation model of Williams didn’t gain traction with the broader investment community until 1959 when it was revived and improved by Myron J. Gordon — thus why it’s called the “Gordon Growth Model”
The Cowles Commission, a bastion of Keynesian Economics, later moved to Yale to follow James Tobin and avoid “increasing friction with the ‘Chicago School’ dominating the economics department” — for students of financial history (or libertarians), yes, this the foreshadowing for everyone’s favorite monetarist which we’ll covered in a later post
The RAND corporation did so much for the fields of mathematics, economics, science, and public policy that it’s difficult to capture. Just check out their “notable members” section on Wikipedia
If you’ve heard the folk legend of the student who arrived late to class, copied some problems down from the board thinking it was homework, and went on to solve previously unsolved equations as homework; that’s Dantzig.
Markowitz (wisely) sidesteps several potential landmines in his paper: security valuation, whether investors truly are rational, non-normal return distributions, and heteroskedasticity of return variance. Economic thinkers have spent the following 70 years debating and theorizing about the nature of these questions and the questions derived from their answers.